ATIVIDADES DA SEMANA DE 07/12 ATÉ 11/12

ALUNOS ATIVIDADES DESTA SEMANA

9º SEMANA DE 07 Á 11/12/2020 do 4º Bimestre)

ENTREGAR ATIVIDADES EM ATRASO E A RECUPERAÇÃO

ATÉ 09/12/2020 NO WHATSAAP PARTICULAR

OU DE 10/12 Á 14/12 PROCURAR A COORDENAÇÃO.

Whatsapp (14) 98122-3831

ATIVIDADES DA SEMANA DE 30/11 ATÉ 04/12

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

07/12/2020

7º SEMANA DE 23 Á 30/11/2020 do 4º Bimestre)

AVISO

NOSSAS ATIVIDADES SÃO DA APOSTILA “APRENDER SEMPRE” E ESTARÁ NO GRUPO DE WHATSAAP DE MATEMÁTICA EM PDF .

QUEM TIVER A APOSTILA EM MÃOS RESPONDER NA PRÓPRIA APOSTILA, SE NÃO COLOCAR SOMENTE AS RESPOSTAS NO CADERNO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 30 Á 07/12/2020 DO

4º BIMESTRE

ATIVIDADES DA APOSTILA “APRENDER SEMPRE”

EXPLICAÇÃO: TEOREMA DE PITÁGORAS

O Teorema de Pitágoras relaciona o comprimento dos lados do triângulo retângulo. Essa figura geométrica é formada por um ângulo interno de 90°, chamado de ângulo reto.
O enunciado desse teorema é:
"A soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa."
Fórmula do teorema de Pitágoras
Segundo o enunciado do Teorema de Pitágoras, a fórmula é representada da seguinte maneira:
a² = b² + c²
Sendo,
a: hipotenusa
b: cateto
c: cateto

A hipotenusa é o maior lado de um triângulo retângulo e o lado oposto ao ângulo reto. Os outros dois lados são os catetos. O ângulo formado por esses dois lados tem medida igual a 90º (ângulo reto).
Identificamos ainda os catetos, de acordo com um ângulo de referência. Ou seja, o cateto poderá ser chamado de cateto adjacente ou cateto oposto.
Quando o cateto está junto ao ângulo de referência, é chamado de adjacente, por outro lado, se está contrário a este ângulo, é chamado de oposto.

Veja a seguir três exemplos de aplicações do teorema de Pitágoras para as relações métricas de um triângulo retângulo.
Exemplo 1: calcular a medida da hipotenusa
Se um triângulo retângulo apresenta 3 cm e 4 cm como medidas dos catetos, qual a hipotenusa desse triângulo?
(Hipotenusa)² = (Cateto1)² + (Cateto2)²
Sendo:
Cateto1 ----> 3cm
Cateto2 ----> 4cm
(Hipotenusa)² = (Cateto1)² + (Cateto2)²
(Hipotenusa)² = (3)² + (4)²
(Hipotenusa)² = (3 . 3) + (4 . 4)
(Hipotenusa)² = 9 + 16
(Hipotenusa)² = 25
Hipotenusa = √25
Hipotenusa = 5
O valor da hipotenusa desse triângulo retângulo é 5cm.
Portanto, os lados do triângulo retângulo são 3 cm, 4 cm e 5 cm.
Exemplo 2: calcular a medida de um dos catetos
Determine a medida de um cateto que faz parte de um triângulo retângulo, cuja hipotenusa é 20 cm e o outro cateto mede 16 cm.
Se a hipotenusa é 20 e um dos catetos é 16, temos que:
20² = 16² + x²
x² = 400 - 256
x² = 144
x = 12
Você também poderia ver que os lados do triângulo são um múltiplo de uma tripla pitagórica: 3,4 e 5. A hipotenusa é 5 x 4 = 20, um cateto é 4 x 4 = 16 e o outro só pode
ser 3 x 4 = 12.

Portanto, as medidas dos lados do triângulo retângulo são 12 cm, 16 cm e 20 cm.

PRAZO DE ENTREGA DAS ATIVIDADES

07/12/2020

Continuação.....

ATIVIDADES : TEOREMA DE PITÁGORAS

Atividade 5 e 6                         apostila pagina 31

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 20/11 ATÉ 27/11

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

30/11/2020

7º SEMANA DE 23 Á 30/11/2020 do 4º Bimestre)

AVISO

NOSSAS ATIVIDADES SÃO DA APOSTILA “APRENDER SEMPRE” E ESTARÁ NO GRUPO DE WHATSAAP DE MATEMÁTICA EM PDF .

QUEM TIVER A APOSTILA EM MÃOS RESPONDER NA PRÓPRIA APOSTILA, SE NÃO COLOCAR SOMENTE AS RESPOSTAS NO CADERNO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 23 Á 30/11/2020 DO

4º BIMESTRE

ATIVIDADES DA APOSTILA “APRENDER SEMPRE”

EXPLICAÇÃO: TEOREMA DE PITÁGORAS

O Teorema de Pitágoras relaciona o comprimento dos lados do triângulo retângulo. Essa figura geométrica é formada por um ângulo interno de 90°, chamado de ângulo reto.

O enunciado desse teorema é:

"A soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa."

Fórmula do teorema de Pitágoras

Segundo o enunciado do Teorema de Pitágoras, a fórmula é representada da seguinte maneira:

a² = b² + c²

Sendo,

a: hipotenusa
b: cateto
c: cateto

A hipotenusa é o maior lado de um triângulo retângulo e o lado oposto ao ângulo reto. Os outros dois lados são os catetos. O ângulo formado por esses dois lados tem medida igual a 90º (ângulo reto).

Identificamos ainda os catetos, de acordo com um ângulo de referência. Ou seja, o cateto poderá ser chamado de cateto adjacente ou cateto oposto.

Quando o cateto está junto ao ângulo de referência, é chamado de adjacente, por outro lado, se está contrário a este ângulo, é chamado de oposto.

Veja a seguir três exemplos de aplicações do teorema de Pitágoras para as relações métricas de um triângulo retângulo.

Exemplo 1: calcular a medida da hipotenusa

Se um triângulo retângulo apresenta 3 cm e 4 cm como medidas dos catetos, qual a hipotenusa desse triângulo?

(Hipotenusa)² = (Cateto1)² + (Cateto2)²

Sendo:

Cateto1 ----> 3cm

Cateto2 ----> 4cm

(Hipotenusa)² = (Cateto1)² + (Cateto2)²

(Hipotenusa)² = (3)² + (4)²

(Hipotenusa)² = (3 . 3) + (4 . 4)

(Hipotenusa)² = 9 + 16

(Hipotenusa)² = 25

Hipotenusa = √25

Hipotenusa = 5

O valor da hipotenusa desse triângulo retângulo é 5cm.

Portanto, os lados do triângulo retângulo são 3 cm, 4 cm e 5 cm.

Exemplo 2: calcular a medida de um dos catetos

Determine a medida de um cateto que faz parte de um triângulo retângulo, cuja hipotenusa é 20 cm e o outro cateto mede 16 cm.

Se a hipotenusa é 20 e um dos catetos é 16, temos que:

20² = 16² + x²

x² = 400 - 256

x² = 144

x = 12

Você também poderia ver que os lados do triângulo são um múltiplo de uma tripla pitagórica: 3,4 e 5. A hipotenusa é 5 x 4 = 20, um cateto é 4 x 4 = 16 e o outro só pode

ser 3 x 4 = 12.

Portanto, as medidas dos lados do triângulo retângulo são 12 cm, 16 cm e 20 cm.

PRAZO DE ENTREGA DAS ATIVIDADES

30/11/2020

ATIVIDADES : TEOREMA DE PITÁGORAS

Atividade 1                               apostila pagina 28

Atividade 2                               apostila pagina 29

Atividade 3 e 4                         apostila pagina 30

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 16/11 ATÉ 20/11
PREZADO ALUNO,

APLICAÇÃO DA AVALIAÇÃO PROCESSUAL, TERÁ INICIO , EM 13/11 ATÉ 23/11/2020,SERÁ ON LINE.
INFORMAMOS DA OBRIGATORIEDADE DA REALIZAÇÃO DA REFERIDA AVALIAÇÃO, PARA EFEITO DE MÉDIA FINAL DO ANO LETIVO DE 2020.
💢A AVALIAÇÃO CONSTITUE DE 26 QUESTÕES DE PORTUGUÊS E 26 DE MATEMÁTICA
💢SIGA AS INSTRUÇÕES PASSO A PASSO PARA ACESSAR A AVALIAÇÃO:
💢ENTRAR NA SED-SECRETARIA ESCOLAR DIGITAL
https://sed.educacao.sp.gov.br/
✔️PREENCHA OS DADOS DE LOGIN E SENHA
LOGIN: (NÚMERO RA)
SENHA: DATA DE NASCIMENTO ( Se não mudou)
✔️NO MENU, SELECIONE AS OPÇOES:
💢 PEDAGÓGICO
💢PLATAFORMA CAED
✔️CLIQUE EM CADERNO
DE ATIVIDADES DE PORTUGUÊS E MATEMÁTICA
✔️CLIQUE EM INICIAR,LEIA COM ATENÇÃO AS QUESTÕES, ESCOLHA A RESPOSTA CORRETA, CLIQUE EM PRÓXIMO
✔️CHEGANDO NA ÚLTIMA QUESTÃO, CLIQUE EM FINALIZAR. APÓS FINALIZAR NÃO PODERÁ RETORNAR A PROVA.
✔️APÓS O INÍCIO DA AVALIAÇÃO   O ALUNO PODERÁ FINALIZAR EM ATÉ 48 HORAS CORRIDAS.
✔️O ALUNO QUE NÃO DISPOR DE RECURSOS TECNOLÓGICOS, PODERÁ FAZER A AVALIAÇÃO NA ESCOLA, NO HORÁRIO DAS 8:00 ÀS 20: 00 HORAS , COM OS COORDENADORES BENILTON OU EDUARDO SEGUINDO O PROTOCOLO DE SEGURANÇA CONTRA O COVID
FONE ESCOLA: 3425-3044
3425-2107

OU PODERÁ REALIZAR A AVALIAÇÃO PELO APLICATIVO CAED:
✔️ABRIR O PLAY STORE GOOGLE
✔️PESQUISAR APLICATIVO:
💢CADERNOS DE ATIVIDADES DE SÃO PAULO( CAED-UFJF)
✔️CLIQUE EM ENTRAR
✔️DIGITAR RA E SENHA
✔️APARECERÁ AS OPÇÕES DE AVALIAÇÃO PORTUGUÊS E MATEMÁTICA
✔️LEIA COM ATENÇÃO , MARCANDO UMA RESPOSTA
✔️O TEMPO SERÁ DE 48 HORAS , PARA RESPONDER ÀS QUESTÕES, APÓS TER INICIADO O TESTE.
✔️FINALIZAR
APÓS FINALIZAR NÃO PODERÁ RETORNAR A PROVA.
✔️CASO VOCÊ TENHA QUALQUER DÚVIDA, PEÇA AJUDA AO SEU PROFESSOR

💢💢💢💢💢💢💢💢

ALUNOS: NÃO DEIXE PARA ÚLTIMA HORA , REALIZE O QUANTO ANTES A AVALIAÇÃO ...
FAÇA COM ATENÇÃO, BOA PROVA❗
💢💢💢💢💢💢💢💢

-Assista ao vídeo para esclarecer suas dúvidas:
https://www.youtube.com/watch?v=j389erhv-QY
https://www.youtube.com/watch?v=oB6uaAx4Tek
ATIVIDADES DA SEMANA DE 09/11 ATÉ 13/11

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

16/11/2020

5º SEMANA DE 09 Á 13/11/2020 do 4º Bimestre)

AVISO

NOSSAS ATIVIDADES SÃO DA APOSTILA “APRENDER SEMPRE” E ESTARÁ NO GRUPO DE WHATSAAP DE MATEMÁTICA EM PDF .

QUEM TIVER A APOSTILA EM MÃOS RESPONDER NA PRÓPRIA APOSTILA, SE NÃO COLOCAR SOMENTE AS RESPOSTAS NO CADERNO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 09 Á 13/11/2020 DO

4º BIMESTRE

ATIVIDADES DA APOSTILA “APRENDER SEMPRE”

EXPLICAÇÃO:

Para falarmos de triângulos precisamos inicialmente recordar sua estrutura. Um triângulo é um polígono que possui: três lados, três vértices e três ângulos internos.

Os triângulos são classificados de acordo com a medida dos seus lados e dos seus ângulos.

A classificação de triângulos em relação aos lados recebe os seguintes nomes: triângulo equilátero, triângulo isósceles e triângulo escaleno. Veja na imagem abaixo a representação desses triângulos.

Quando a classificação de triângulos é feita em relação às medidas dos ângulos internos são nomeados da seguinte forma: triângulo acutângulo, triângulo retângulo e triângulo obtusângulo.

Agora que você já sabe quais são as possíveis classificações para triângulos, observe os objetos a sua volta e os identifique. Ficará surpreso ao descobrir que a nossa realidade está cheia deles.

Os triângulos são figuras geométricas que podem ser classificadas de acordo com as medidas de seus lados e seus ângulos

PRAZO DE ENTREGA DAS ATIVIDADES

16/11/2020

ATIVIDADES

OS TRIÂNGULOS E SUAS CLASSIFICAÇÕES

Atividade 1                               apostila pagina 23

Atividade 2 e 3                         apostila pagina 24

Atividade 4 e 5                         apostila pagina 25

Atividade 6                               apostila pagina 26

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 03/11 ATÉ 06/11

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

09/11/2020

4º SEMANA DE 03 Á 06/11/2020 do 4º Bimestre)

AVISO

O CADERNO DO ALUNO REFERENTE AO 4º BIMESTRE ESTÁ DISPONÍVEL NA ESCOLA NO HORÁRIO DAS 8H ATÉ AS 21H

OBS: A APOSTILA CADERNO DO ALUNO VOL.04 ESTARÁ NO GRUPO DE WHATSAAP DE MATEMÁTICA

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, AQUELES QUE PEGAREM A APOSTILA E TIVER ESPAÇO PARA RESOLVER AS ATIVIDADES NELA PODE FAZER.

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 03 Á 06/11/2020 DO

4º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 4

EXPLICAÇÃO: PRISMAS: UMA FORMA DE OCUPAR O ESPAÇO

Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas características básicas definem esse sólido geométrico. Por exemplo, o número de faces do prisma será exatamente igual ao número de lados do polígono que constitui suas bases (superior e inferior), dessa forma, sua classificação quanto ao número de lados pode ser:

Triangular – base constituída de triângulos.
Quadrangular – base constituída de quadriláteros.
Pentagonal – base constituída de pentágonos.
Hexagonal – base constituída de hexágonos.
Heptagonal – base constituída de heptágonos.
Octogonal – base constituída de octógonos.

Os prismas também podem ser classificados como retos ou oblíquos. Os prismas retos são aqueles em que a aresta lateral forma com a base um ângulo de 90º, os oblíquos são aqueles em que as arestas formam ângulos diferentes de 90º.

Todos os prismas possuem área da base, área lateral, área total e volume. Todas essas medidas dependem do formato do polígono que se encontra nas bases; por exemplo, os prismas acima possuem em sua base um pentágono, portanto, para calcularmos a área dessa base devemos determinar a área do pentágono. No caso do prisma pentagonal reto, as faces laterais constituem retângulos e a do prisma oblíquo é formada por paralelogramos.
A área total de um prisma é calculada somando a área lateral e o dobro da área da base. E o volume é determinado calculando a área da base multiplicada pela medida da altura.

Observe alguns exemplos de prismas:

Prisma Triangular Reto

Prisma Hexagonal Reto

Prisma Pentagonal Oblíquo

Prisma Quadrangular Oblíquo

EXEMPLOS: Qual o volume de concreto utilizado na construção de uma laje de 80 centímetros de espessura em uma sala com medidas iguais a 4 metros de largura e 6 metros de comprimento?

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

09/11/2020

ATIVIDADES

TEMA 1 - PRISMAS: UMA FORMA DE OCUPAR O ESPAÇO

Atividade 1 e 2                          apostila pagina 161

Atividade 3 e 4                          apostila pagina 162

Atividade 5                                apostila pagina 163

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 26/10 ATÉ 30/10

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

03/11/2020

3º SEMANA DE 26 Á 30/10/2020 do 4º Bimestre)

NOSSAS ATIVIDADES SEGUEM O CADERNO DO ALUNO

VOL. 3

AVISO

O CADERNO DO ALUNO REFERENTE AO 4º BIMESTRE ESTÁ DISPONÍVEL NA ESCOLA NO HORÁRIO DAS 8H ATÉ AS 21H

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, AQUELES QUE PEGAREM A APOSTILA E TIVER ESPAÇO PARA RESOLVER AS ATIVIDADES NELA PODE FAZER.

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 26 Á 30/10/2020 DO

4º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO: ESTUDANDO AS PROBABILIDADES

A probabilidade simplesmente determina qual é a chance de algo acontecer. Toda vez que não temos certeza sobre o resultado de algum evento, estamos tratando da probabilidade de certos resultados acontecerem—ou quais as chances de eles acontecerem. A análise de eventos determinados pela probabilidade é chamada de estatística.

O melhor exemplo para entender probabilidade é o cara-ou-coroa:

Temos dois resultados possíveis—cara-ou-coroa.

Qual é a probabilidade de virar cara? Podemos descobrir ao usar uma equação. Pode ser que, intuitivamente, você já saiba que as chances são meio a meio, ou seja, 50%. Mas como desenvolver isso? Probabilidade =

Neste caso:

Probabilidade de um evento = (nº de maneiras possíveis de ele acontecer) / (número total de resultados)

P(A) = (nº de maneiras que A pode acontecer) / (Número total de resultados)

Exemplo 1

Temos seis resultados diferentes.

Diferentes resultados ao se jogar um dado

Qual é a probabilidade de obtermos o número um?

Fórmula da probabilidade de tirar 1 no dado

Qual é a probabilidade de obtermos o número um ou o número 6?

Probabilidade de tirar 1 ou 6 no dado

Usando a fórmula acima:

Fórmula da probabilidade aplicada

Qual é a probabilidade de obtermos um número par? (ou seja, 2, 4 ou 6)

Dicas

·         A probabilidade de um evento só pode estar entre 0 e 1 e pode ser escrita, também, como um percentual.

·         A probabilidade do evento A é muitas vezes escrita como P(A).

·         Se P(A) > P(B) então o evento A tem uma maior chance de ocorrer que o evento B.

·         Se P(A) = P(B), então os eventos A e B  têm chances iguais de acontecer.

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

03/11/2020

ATIVIDADES

TEMA 4 : ESTUDANDO AS PROBABILIDADES

Atividade 1 (somente leitura)    apostila pagina 18

Atividade 2 e 3                          apostila pagina 19

Atividade 4 e 5                          apostila pagina 20

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 16/10 ATÉ 23/10

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

26/10/2020

2º SEMANA DE 19 Á 23/10/2020 do 4º Bimestre)

NOSSAS ATIVIDADES SEGUEM O CADERNO DO ALUNO

VOL. 3

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, AQUELES QUE PEGAREM A APOSTILA E TIVER ESPAÇO PARA RESOLVER AS ATIVIDADES NELA PODE FAZER.

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 19 Á 23/10/2020 DO 4º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO DA SEMANA ANTERIOR........ CONTINUAÇÃO DAS ATIVIDADES

EXPLICAÇÃO: Análise Combinatória, Probabilidade

A análise combinatória é a área da Matemática que tem como função estudar a quantidade de agrupamentos que podem ser formados a partir de um conjunto de valores. O foco é o estudo dos tipos de agrupamento, que são resolvidos pelo princípio fundamental da contagem. Esses agrupamentos são a permutação, a combinação e o arranjo. Cada tipo tem aplicações específicas, e o que determina qual deve ser usado é a situação em que se encontram e o objetivo da contagem. Qual é a função da análise combinatória?
Como o nome sugere, a análise combinatória tem como função analisar e contar todas as combinações possíveis. Os agrupamentos estão constantemente presentes no nosso dia a dia e prever essas combinações é fundamental para a tomada de decisões.
Você já se perguntou quantos resultados podem ser obtidos na loteria? Ou a quantidade de senhas possíveis para que a sua senha de banco seja segura? A combinação faz parte do nosso cotidiano, desde objetos simples, como a placa de um carro – que deve ser única por estado –, o Cadastro de Pessoa Física (CPF), que é único por cidadão, até as decisões mais complexas, como algoritmos de programação, investimentos em bolsas etc. Além disso, a análise combinatória dá suporte para outras áreas de conhecimento e para estudos mais aprofundados na própria matemática.
Princípio fundamental da contagem
Base para a análise combinatória, o princípio fundamental da contagem é uma forma rápida de calcular a quantidade de combinações possíveis para determinadas decisões. Conhecido também como PFC, esse princípio diz o seguinte:
Se uma decisão d₁ pode ser tomada de n maneiras e uma decisão d₂ pode ser tomada de m maneiras, e essas decisões são independentes entre si, então o número de combinações possíveis entre essas duas decisões é calculado por (n · m).
A aplicação do princípio fundamental da contagem é bastante simples quando se entende bem a situação proposta, o que pode dificultar muito é a interpretação do problema, e não o cálculo em si.
·         Exemplo
Em uma sanduicheria, os sanduíches são vendidos em combos. O cliente pode escolher um entre três tipos de carne (frango, porco ou bovina), um entre três tipos de queijo (muçarela, cheddar ou prato) e um entre dois tipos de bebidas (refrigerante e suco). Sendo assim, quantas vezes um cliente pode pedir um combo sem repeti-lo?
Resolução 1:
Sem usar o princípio fundamental da contagem, uma forma de resolução possível é realizar a listagem das escolhas e contar o número de possibilidades.
Ao todo o cliente terá que tomar três decisões (carne, queijo, bebida). Podemos listar todas as possibilidades por meio de uma tabela, lista ou diagrama. O problema é que esse processo se torna cada vez mais trabalhoso quando a quantidade de possibilidades para cada decisão aumenta.

Resolução 2:
Pelo princípio fundamental da contagem, chegamos à mesma quantidade, mas sem a necessidade de fazer a lista de todas as possibilidades. Sabemos que há três decisões a serem tomadas, então o número de possibilidades é igual ao produto das possibilidades de cada uma dessas decisões:
·         3 tipos de carne
·         3 tipos de queijo
·         2 tipos de bebidas
3.3.2 = 18 possibilidades
Fatorial de um número
A multiplicação de um número por seus antecessores é bastante recorrente em problemas que envolvem análise combinatória, e é importante compreender as operações com fatorial e também as possíveis simplificações.
Seja n um número natural maior que 2, chamamos de n! (n fatorial) a operação:
n! = n. (n-1). (n-2) . … 3. 2 .1
·         Exemplos
5! = 5.4.3.2.1= 120
10! = 10 . 9. 8 . 7 .6 .5 .4. 3. 2. 1 = 3.628.800
Por definição, temos que:
0!=1
1!=1
Tipos de agrupamentos
Os agrupamentos estudados na análise combinatória são a permutação, combinação e arranjo. Cada um deles é empregado em uma situação e possui métodos específicos para ser calculado. O que deve ficar claro é quando devemos escolher o agrupamento e como realizar o cálculo.
·         Permutação
Conhecemos como permutação os agrupamentos ordenados de todos os elementos de um conjunto. Permutar é trocar de posição, formando uma nova ordem.
A permutação de um conjunto com n elementos é calculada por:
P = n!
Aplicações: problemas que envolvem anagramas, filas, posições.
Lembre-se de que, para ser permutação, todos os elementos do conjunto devem ser utilizados. Além disso, a ordem dos elementos é importante.
·         Exemplo
Quantos anagramas existem na palavra AMOR?
Anagrama nada mais é do que a troca de posição entre as letras da palavra, formando novas palavras, que podem fazer sentido ou não na nossa língua. Esse problema é uma permutação porque estamos calculando todos os agrupamentos possíveis ao mudar a ordem de todos os elementos do conjunto.
Resolução 1 (pelo PFC):
A palavra AMOR possui 4 letras. Pelo PFC vamos tomar 4 decisões, ou seja, escolher a primeira, segunda, terceira e quarta letra.
·         1ª letra: Para escolher a primeira letra, há quatro possibilidades (A, M, O, R).
·         2ª letra: Como escolhemos uma letra na primeira, restam três possibilidades, independentemente da escolha.
·         3ª letra: Como escolhemos uma letra na primeira e outra na segunda posição, restam duas possibilidades, independentemente das escolhas.
·         4ª letra: Como já escolhemos três letras (primeira, segunda e terceira posição), resta apenas uma possibilidade para a quarta letra.
Pelo PFC o número de anagramas da palavra amor será calculado por: 4.3.2.1. Esse produto é igual a 24 possibilidades.
Resolução 2:
Vale ressaltar que a fórmula da permutação resulta do princípio fundamental da contagem, logo ela pode ser utilizada de forma direta.
Como a palavra AMOR tem quatro letras, o total de anagramas possíveis é dado pela permutação de quatro elementos.
A permutação P₄=4! = 4.3.2.1= 24 possibilidades.
·         Arranjo
Entendemos como a rranjo s os agrupamentos ordenados formados por parte dos elementos de um conjunto. Dado um conjunto de n elementos, queremos saber quantos agrupamentos ordenados podemos formar com p elementos, sendo p sempre menor que n. Perceba a diferença entre o arranjo e a permutação – em ambos a ordem é importante, mas na permutação agrupamos todos os elementos do conjunto, já no arranjo agrupamos apenas parte desses elementos.

·         Exemplo
O conselho de uma escola organizou-se para escolher os ocupantes dos cargos administrativos mais importantes. Esses cargos seriam escolhidos a partir de votação de todos os membros do conselho. Os cargos da instituição são diretor, secretário e coordenador financeiro. Em cada voto será colocado o trio que ocupará cada um dos cargos. Sabendo que há 5 candidatos possíveis para cada uma das vagas, o número de comissões administrativas possíveis é?
Analisando o problema:
Ao analisar situações-problema que envolvem análise combinatória, é importante identificar o agrupamento. Perceba que será feita uma escolha de 3 entre 5 possibilidades. Note também que a ordem é importante. Por exemplo, o voto para Aline, Brenda e Cláudio não é o mesmo que o voto para Cláudio, Aline e Brenda – nesse caso, já que são atribuídas funções para cada um deles, por mais que a comissão seja formada pelos mesmos três candidatos, a ordem é importante, o que torna essa questão um problema de arranjo.
Resolução:
n = 5 e p = 3
Logo queremos calcular:

Veja também: Critérios para identificação de arranjo ou combinação
·         Combinação
A combinação é um agrupamento que está ligado a subconjuntos de um conjunto. Entendemos como combinação de n, tomados de p em p, a contagem de todos os subconjuntos possíveis com p elementos de n. A diferença entre a combinação e o arranjo é que, na combinação, a ordem não é importante, então os conjuntos {A,B,C} e {C,A,B} são os mesmos conjuntos.
Para calcular a c ombinação, utilizamos a fórmula:

·         Exemplo
Para a organização da colação de grau, os estudantes decidiram montar uma comissão de formatura. Sabendo que havia 30 formandos e que somente 2 alunos seriam escolhidos, a quantidade de comissões possíveis será?
Analisando o problema:
Ao analisar situações-problema que envolvem análise combinatória, é importante identificar o agrupamento. Perceba que será feita uma escolha de 2 entre 30 possibilidades. Além disso, é possível perceber que a ordem não é importante, pois se a comissão for composta por {Robson, Kleyton} ou {Kleyton, Robson}, por exemplo, não haverá diferença alguma. Como a ordem não importa e estamos escolhendo subconjuntos de um conjunto de 30 possibilidades, esse problema deve ser resolvido por combinação.
Resolução:

Análise combinatória e probabilidade
Probabilidade é uma importantíssima área da Matemática e determina a chance de um evento ocorrer. Estamos cercados por probabilidade nas lotéricas, nos jogos de dados, cartas, entre várias outras situações. Para estudarmos probabilidade a fundo, é fundamental o domínio dos conceitos da análise combinatória, pois a probabilidade de um evento acontecer é a razão entre a contagem de todos os casos favoráveis sob a contagem de todos os casos possíveis.
Assim, problemas que envolvem probabilidade podem também necessariamente envolver uma situação de análise combinatória. Percebemos, então, que a análise combinatória é um pré-requisito para o aprendizado da probabilidade, oferecendo ferramentas importantes para a contagem tanto dos casos favoráveis como dos casos possíveis.
·         Exemplo
Em uma turma de Inglês, será sorteada para três estudantes uma viagem com tudo pago para a cidade de Caldas Novas. Sabendo que no curso há 12 alunos e que 5 são meninos, qual é a probabilidade de a dupla sorteada ser composta por duas meninas?
Resolução
Para calcular a probabilidade, precisamos antes contar todas os trios possíveis e também calcular todos os trios formadas por duas meninas. Como a ordem não é importante, podemos usar combinação.
1º passo – Todos os trios possíveis
·         n= 12 (todos os alunos)
·         p = 3 (quantidade de alunos a serem escolhidos)

2º passo – Todos os trios formados por duas meninas
·         n = 12 – 5→ n = 7 (total de meninas)
·         p=3 (quantidade de alunos a serem escolhidos)

3º passo - Cálculo da probabilidade

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

26/10/2020

ATIVIDADES

TEMA 3 : Formação de Grupos com elementos de uma ou mais categorias – PG. 14

Atividade 27, 28, 29 e 30 apostila pagina 17

Atividade 31                     apostila pagina 18

Whatsapp (14) 98122-3831 ou   Classroon

  ATIVIDADES DA SEMANA 13/10 ATÉ 16/10

  ATENÇÃO ALUNOS



PRAZO DE ENTREGA DAS ATIVIDADES

19/10/2020

1º SEMANA DE 13 Á 16/10/2020 (está semana constará no 4º Bimestre)

NOSSAS ATIVIDADES SEGUEM O CADERNO DO ALUNO

VOL. 3

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, AQUELES QUE PEGAREM A APOSTILA E TIVER ESPAÇO PARA RESOLVER AS ATIVIDADES NELA PODE FAZER.

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.



Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 13 Á 16/10/2020 CONSTARÁ NO 4º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO DA SEMANA ANTERIOR........ CONTINUAÇÃO DAS ATIVIDADES

EXPLICAÇÃO: Análise Combinatória, Probabilidade

A análise combinatória é a área da Matemática que tem como função estudar a quantidade de agrupamentos que podem ser formados a partir de um conjunto de valores. O foco é o estudo dos tipos de agrupamento, que são resolvidos pelo princípio fundamental da contagem. Esses agrupamentos são a permutação, a combinação e o arranjo. Cada tipo tem aplicações específicas, e o que determina qual deve ser usado é a situação em que se encontram e o objetivo da contagem. Qual é a função da análise combinatória?
Como o nome sugere, a análise combinatória tem como função analisar e contar todas as combinações possíveis. Os agrupamentos estão constantemente presentes no nosso dia a dia e prever essas combinações é fundamental para a tomada de decisões.
Você já se perguntou quantos resultados podem ser obtidos na loteria? Ou a quantidade de senhas possíveis para que a sua senha de banco seja segura? A combinação faz parte do nosso cotidiano, desde objetos simples, como a placa de um carro – que deve ser única por estado –, o Cadastro de Pessoa Física (CPF), que é único por cidadão, até as decisões mais complexas, como algoritmos de programação, investimentos em bolsas etc. Além disso, a análise combinatória dá suporte para outras áreas de conhecimento e para estudos mais aprofundados na própria matemática.
Princípio fundamental da contagem
Base para a análise combinatória, o princípio fundamental da contagem é uma forma rápida de calcular a quantidade de combinações possíveis para determinadas decisões. Conhecido também como PFC, esse princípio diz o seguinte:
Se uma decisão d₁ pode ser tomada de n maneiras e uma decisão d₂ pode ser tomada de m maneiras, e essas decisões são independentes entre si, então o número de combinações possíveis entre essas duas decisões é calculado por (n · m).
A aplicação do princípio fundamental da contagem é bastante simples quando se entende bem a situação proposta, o que pode dificultar muito é a interpretação do problema, e não o cálculo em si.
·         Exemplo
Em uma sanduicheria, os sanduíches são vendidos em combos. O cliente pode escolher um entre três tipos de carne (frango, porco ou bovina), um entre três tipos de queijo (muçarela, cheddar ou prato) e um entre dois tipos de bebidas (refrigerante e suco). Sendo assim, quantas vezes um cliente pode pedir um combo sem repeti-lo?
Resolução 1:
Sem usar o princípio fundamental da contagem, uma forma de resolução possível é realizar a listagem das escolhas e contar o número de possibilidades.
Ao todo o cliente terá que tomar três decisões (carne, queijo, bebida). Podemos listar todas as possibilidades por meio de uma tabela, lista ou diagrama. O problema é que esse processo se torna cada vez mais trabalhoso quando a quantidade de possibilidades para cada decisão aumenta.

Resolução 2:
Pelo princípio fundamental da contagem, chegamos à mesma quantidade, mas sem a necessidade de fazer a lista de todas as possibilidades. Sabemos que há três decisões a serem tomadas, então o número de possibilidades é igual ao produto das possibilidades de cada uma dessas decisões:
·         3 tipos de carne
·         3 tipos de queijo
·         2 tipos de bebidas
3.3.2 = 18 possibilidades
Fatorial de um número
A multiplicação de um número por seus antecessores é bastante recorrente em problemas que envolvem análise combinatória, e é importante compreender as operações com fatorial e também as possíveis simplificações.
Seja n um número natural maior que 2, chamamos de n! (n fatorial) a operação:
n! = n. (n-1). (n-2) . … 3. 2 .1
·         Exemplos
5! = 5.4.3.2.1= 120
10! = 10 . 9. 8 . 7 .6 .5 .4. 3. 2. 1 = 3.628.800
Por definição, temos que:
0!=1
1!=1
Tipos de agrupamentos
Os agrupamentos estudados na análise combinatória são a permutação, combinação e arranjo. Cada um deles é empregado em uma situação e possui métodos específicos para ser calculado. O que deve ficar claro é quando devemos escolher o agrupamento e como realizar o cálculo.
·         Permutação
Conhecemos como permutação os agrupamentos ordenados de todos os elementos de um conjunto. Permutar é trocar de posição, formando uma nova ordem.
A permutação de um conjunto com n elementos é calculada por:
P = n!
Aplicações: problemas que envolvem anagramas, filas, posições.
Lembre-se de que, para ser permutação, todos os elementos do conjunto devem ser utilizados. Além disso, a ordem dos elementos é importante.
·         Exemplo
Quantos anagramas existem na palavra AMOR?
Anagrama nada mais é do que a troca de posição entre as letras da palavra, formando novas palavras, que podem fazer sentido ou não na nossa língua. Esse problema é uma permutação porque estamos calculando todos os agrupamentos possíveis ao mudar a ordem de todos os elementos do conjunto.
Resolução 1 (pelo PFC):
A palavra AMOR possui 4 letras. Pelo PFC vamos tomar 4 decisões, ou seja, escolher a primeira, segunda, terceira e quarta letra.
·         1ª letra: Para escolher a primeira letra, há quatro possibilidades (A, M, O, R).
·         2ª letra: Como escolhemos uma letra na primeira, restam três possibilidades, independentemente da escolha.
·         3ª letra: Como escolhemos uma letra na primeira e outra na segunda posição, restam duas possibilidades, independentemente das escolhas.
·         4ª letra: Como já escolhemos três letras (primeira, segunda e terceira posição), resta apenas uma possibilidade para a quarta letra.
Pelo PFC o número de anagramas da palavra amor será calculado por: 4.3.2.1. Esse produto é igual a 24 possibilidades.
Resolução 2:
Vale ressaltar que a fórmula da permutação resulta do princípio fundamental da contagem, logo ela pode ser utilizada de forma direta.
Como a palavra AMOR tem quatro letras, o total de anagramas possíveis é dado pela permutação de quatro elementos.
A permutação P₄=4! = 4.3.2.1= 24 possibilidades.
·         Arranjo
Entendemos como a rranjo s os agrupamentos ordenados formados por parte dos elementos de um conjunto. Dado um conjunto de n elementos, queremos saber quantos agrupamentos ordenados podemos formar com p elementos, sendo p sempre menor que n. Perceba a diferença entre o arranjo e a permutação – em ambos a ordem é importante, mas na permutação agrupamos todos os elementos do conjunto, já no arranjo agrupamos apenas parte desses elementos.

·         Exemplo
O conselho de uma escola organizou-se para escolher os ocupantes dos cargos administrativos mais importantes. Esses cargos seriam escolhidos a partir de votação de todos os membros do conselho. Os cargos da instituição são diretor, secretário e coordenador financeiro. Em cada voto será colocado o trio que ocupará cada um dos cargos. Sabendo que há 5 candidatos possíveis para cada uma das vagas, o número de comissões administrativas possíveis é?
Analisando o problema:
Ao analisar situações-problema que envolvem análise combinatória, é importante identificar o agrupamento. Perceba que será feita uma escolha de 3 entre 5 possibilidades. Note também que a ordem é importante. Por exemplo, o voto para Aline, Brenda e Cláudio não é o mesmo que o voto para Cláudio, Aline e Brenda – nesse caso, já que são atribuídas funções para cada um deles, por mais que a comissão seja formada pelos mesmos três candidatos, a ordem é importante, o que torna essa questão um problema de arranjo.
Resolução:
n = 5 e p = 3
Logo queremos calcular:

Veja também: Critérios para identificação de arranjo ou combinação
·         Combinação
A combinação é um agrupamento que está ligado a subconjuntos de um conjunto. Entendemos como combinação de n, tomados de p em p, a contagem de todos os subconjuntos possíveis com p elementos de n. A diferença entre a combinação e o arranjo é que, na combinação, a ordem não é importante, então os conjuntos {A,B,C} e {C,A,B} são os mesmos conjuntos.
Para calcular a c ombinação, utilizamos a fórmula:

·         Exemplo
Para a organização da colação de grau, os estudantes decidiram montar uma comissão de formatura. Sabendo que havia 30 formandos e que somente 2 alunos seriam escolhidos, a quantidade de comissões possíveis será?
Analisando o problema:
Ao analisar situações-problema que envolvem análise combinatória, é importante identificar o agrupamento. Perceba que será feita uma escolha de 2 entre 30 possibilidades. Além disso, é possível perceber que a ordem não é importante, pois se a comissão for composta por {Robson, Kleyton} ou {Kleyton, Robson}, por exemplo, não haverá diferença alguma. Como a ordem não importa e estamos escolhendo subconjuntos de um conjunto de 30 possibilidades, esse problema deve ser resolvido por combinação.
Resolução:

Análise combinatória e probabilidade
Probabilidade é uma importantíssima área da Matemática e determina a chance de um evento ocorrer. Estamos cercados por probabilidade nas lotéricas, nos jogos de dados, cartas, entre várias outras situações. Para estudarmos probabilidade a fundo, é fundamental o domínio dos conceitos da análise combinatória, pois a probabilidade de um evento acontecer é a razão entre a contagem de todos os casos favoráveis sob a contagem de todos os casos possíveis.
Assim, problemas que envolvem probabilidade podem também necessariamente envolver uma situação de análise combinatória. Percebemos, então, que a análise combinatória é um pré-requisito para o aprendizado da probabilidade, oferecendo ferramentas importantes para a contagem tanto dos casos favoráveis como dos casos possíveis.
·         Exemplo
Em uma turma de Inglês, será sorteada para três estudantes uma viagem com tudo pago para a cidade de Caldas Novas. Sabendo que no curso há 12 alunos e que 5 são meninos, qual é a probabilidade de a dupla sorteada ser composta por duas meninas?
Resolução
Para calcular a probabilidade, precisamos antes contar todas os trios possíveis e também calcular todos os trios formadas por duas meninas. Como a ordem não é importante, podemos usar combinação.
1º passo – Todos os trios possíveis
·         n= 12 (todos os alunos)
·         p = 3 (quantidade de alunos a serem escolhidos)

2º passo – Todos os trios formados por duas meninas
·         n = 12 – 5→ n = 7 (total de meninas)
·         p=3 (quantidade de alunos a serem escolhidos)

3º passo - Cálculo da probabilidade

ATENÇÃO ALUNOS

PRAZO DE ENTREGA DAS ATIVIDADES

19/10/2020

ATIVIDADES

TEMA 3 : Formação de Grupos com elementos de uma ou mais categorias – PG. 14

Atividade 23, 24, 25 e 26 apostila pagina 16

OBS: ATIVIDADE 25 SERÁ FEITA INDIVIDUALMENTE, E NÃO PRECISA TROCAR O EXERCÍCIO.

ELABORE E RESOLVA INDIVIDUALMENTE.

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA SEMANA DE 28/09 ATÉ 02/10
ATENÇÃO ALUNOS

ESTAMOS NA 9ª SEMANA DO 3º BIMESTRE

O CADERNO DO ALUNO VOL. 03 ESTÃO DISPONIVÉIS PARA SEREM RETIRADOS NA ESCOLA DESDE 01/09/2020
HORÁRIO DAS 10H ÁS 16H

TERÇA E QUINTA FEIRA ABERTO AO PÚBLICO

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, NÃO HÁ ESPAÇO PARA RESOLVER NO CADERNO

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp ou Classroon , ENVIAR A FOTO.

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES DA 9ª SEMANA DO 3º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO: Análise Combinatória, Probabilidade

A análise combinatória é a área da Matemática que tem como função estudar a quantidade de agrupamentos que podem ser formados a partir de um conjunto de valores. O foco é o estudo dos tipos de agrupamento, que são resolvidos pelo princípio fundamental da contagem. Esses agrupamentos são a permutação, a combinação e o arranjo. Cada tipo tem aplicações específicas, e o que determina qual deve ser usado é a situação em que se encontram e o objetivo da contagem. Qual é a função da análise combinatória?
Como o nome sugere, a análise combinatória tem como função analisar e contar todas as combinações possíveis. Os agrupamentos estão constantemente presentes no nosso dia a dia e prever essas combinações é fundamental para a tomada de decisões.
Você já se perguntou quantos resultados podem ser obtidos na loteria? Ou a quantidade de senhas possíveis para que a sua senha de banco seja segura? A combinação faz parte do nosso cotidiano, desde objetos simples, como a placa de um carro – que deve ser única por estado –, o Cadastro de Pessoa Física (CPF), que é único por cidadão, até as decisões mais complexas, como algoritmos de programação, investimentos em bolsas etc. Além disso, a análise combinatória dá suporte para outras áreas de conhecimento e para estudos mais aprofundados na própria matemática.
Princípio fundamental da contagem
Base para a análise combinatória, o princípio fundamental da contagem é uma forma rápida de calcular a quantidade de combinações possíveis para determinadas decisões. Conhecido também como PFC, esse princípio diz o seguinte:
Se uma decisão d₁ pode ser tomada de n maneiras e uma decisão d₂ pode ser tomada de m maneiras, e essas decisões são independentes entre si, então o número de combinações possíveis entre essas duas decisões é calculado por (n · m).
A aplicação do princípio fundamental da contagem é bastante simples quando se entende bem a situação proposta, o que pode dificultar muito é a interpretação do problema, e não o cálculo em si.
·         Exemplo
Em uma sanduicheria, os sanduíches são vendidos em combos. O cliente pode escolher um entre três tipos de carne (frango, porco ou bovina), um entre três tipos de queijo (muçarela, cheddar ou prato) e um entre dois tipos de bebidas (refrigerante e suco). Sendo assim, quantas vezes um cliente pode pedir um combo sem repeti-lo?
Resolução 1:
Sem usar o princípio fundamental da contagem, uma forma de resolução possível é realizar a listagem das escolhas e contar o número de possibilidades.
Ao todo o cliente terá que tomar três decisões (carne, queijo, bebida). Podemos listar todas as possibilidades por meio de uma tabela, lista ou diagrama. O problema é que esse processo se torna cada vez mais trabalhoso quando a quantidade de possibilidades para cada decisão aumenta.

Resolução 2:
Pelo princípio fundamental da contagem, chegamos à mesma quantidade, mas sem a necessidade de fazer a lista de todas as possibilidades. Sabemos que há três decisões a serem tomadas, então o número de possibilidades é igual ao produto das possibilidades de cada uma dessas decisões:
·         3 tipos de carne
·         3 tipos de queijo
·         2 tipos de bebidas
3.3.2 = 18 possibilidades
Fatorial de um número
A multiplicação de um número por seus antecessores é bastante recorrente em problemas que envolvem análise combinatória, e é importante compreender as operações com fatorial e também as possíveis simplificações.
Seja n um número natural maior que 2, chamamos de n! (n fatorial) a operação:
n! = n. (n-1). (n-2) . … 3. 2 .1
·         Exemplos
5! = 5.4.3.2.1= 120
10! = 10 . 9. 8 . 7 .6 .5 .4. 3. 2. 1 = 3.628.800
Por definição, temos que:
0!=1
1!=1
Tipos de agrupamentos
Os agrupamentos estudados na análise combinatória são a permutação, combinação e arranjo. Cada um deles é empregado em uma situação e possui métodos específicos para ser calculado. O que deve ficar claro é quando devemos escolher o agrupamento e como realizar o cálculo.
·         Permutação
Conhecemos como permutação os agrupamentos ordenados de todos os elementos de um conjunto. Permutar é trocar de posição, formando uma nova ordem.
A permutação de um conjunto com n elementos é calculada por:
P = n!
Aplicações: problemas que envolvem anagramas, filas, posições.
Lembre-se de que, para ser permutação, todos os elementos do conjunto devem ser utilizados. Além disso, a ordem dos elementos é importante.
·         Exemplo
Quantos anagramas existem na palavra AMOR?
Anagrama nada mais é do que a troca de posição entre as letras da palavra, formando novas palavras, que podem fazer sentido ou não na nossa língua. Esse problema é uma permutação porque estamos calculando todos os agrupamentos possíveis ao mudar a ordem de todos os elementos do conjunto.
Resolução 1 (pelo PFC):
A palavra AMOR possui 4 letras. Pelo PFC vamos tomar 4 decisões, ou seja, escolher a primeira, segunda, terceira e quarta letra.
·         1ª letra: Para escolher a primeira letra, há quatro possibilidades (A, M, O, R).
·         2ª letra: Como escolhemos uma letra na primeira, restam três possibilidades, independentemente da escolha.
·         3ª letra: Como escolhemos uma letra na primeira e outra na segunda posição, restam duas possibilidades, independentemente das escolhas.
·         4ª letra: Como já escolhemos três letras (primeira, segunda e terceira posição), resta apenas uma possibilidade para a quarta letra.
Pelo PFC o número de anagramas da palavra amor será calculado por: 4.3.2.1. Esse produto é igual a 24 possibilidades.
Resolução 2:
Vale ressaltar que a fórmula da permutação resulta do princípio fundamental da contagem, logo ela pode ser utilizada de forma direta.
Como a palavra AMOR tem quatro letras, o total de anagramas possíveis é dado pela permutação de quatro elementos.
A permutação P₄=4! = 4.3.2.1= 24 possibilidades.
·         Arranjo
Entendemos como a rranjo s os agrupamentos ordenados formados por parte dos elementos de um conjunto. Dado um conjunto de n elementos, queremos saber quantos agrupamentos ordenados podemos formar com p elementos, sendo p sempre menor que n. Perceba a diferença entre o arranjo e a permutação – em ambos a ordem é importante, mas na permutação agrupamos todos os elementos do conjunto, já no arranjo agrupamos apenas parte desses elementos.

·         Exemplo
O conselho de uma escola organizou-se para escolher os ocupantes dos cargos administrativos mais importantes. Esses cargos seriam escolhidos a partir de votação de todos os membros do conselho. Os cargos da instituição são diretor, secretário e coordenador financeiro. Em cada voto será colocado o trio que ocupará cada um dos cargos. Sabendo que há 5 candidatos possíveis para cada uma das vagas, o número de comissões administrativas possíveis é?
Analisando o problema:
Ao analisar situações-problema que envolvem análise combinatória, é importante identificar o agrupamento. Perceba que será feita uma escolha de 3 entre 5 possibilidades. Note também que a ordem é importante. Por exemplo, o voto para Aline, Brenda e Cláudio não é o mesmo que o voto para Cláudio, Aline e Brenda – nesse caso, já que são atribuídas funções para cada um deles, por mais que a comissão seja formada pelos mesmos três candidatos, a ordem é importante, o que torna essa questão um problema de arranjo.
Resolução:
n = 5 e p = 3
Logo queremos calcular:

Veja também: Critérios para identificação de arranjo ou combinação
·         Combinação
A combinação é um agrupamento que está ligado a subconjuntos de um conjunto. Entendemos como combinação de n, tomados de p em p, a contagem de todos os subconjuntos possíveis com p elementos de n. A diferença entre a combinação e o arranjo é que, na combinação, a ordem não é importante, então os conjuntos {A,B,C} e {C,A,B} são os mesmos conjuntos.
Para calcular a c ombinação, utilizamos a fórmula:

·         Exemplo
Para a organização da colação de grau, os estudantes decidiram montar uma comissão de formatura. Sabendo que havia 30 formandos e que somente 2 alunos seriam escolhidos, a quantidade de comissões possíveis será?
Analisando o problema:
Ao analisar situações-problema que envolvem análise combinatória, é importante identificar o agrupamento. Perceba que será feita uma escolha de 2 entre 30 possibilidades. Além disso, é possível perceber que a ordem não é importante, pois se a comissão for composta por {Robson, Kleyton} ou {Kleyton, Robson}, por exemplo, não haverá diferença alguma. Como a ordem não importa e estamos escolhendo subconjuntos de um conjunto de 30 possibilidades, esse problema deve ser resolvido por combinação.
Resolução:

Análise combinatória e probabilidade
Probabilidade é uma importantíssima área da Matemática e determina a chance de um evento ocorrer. Estamos cercados por probabilidade nas lotéricas, nos jogos de dados, cartas, entre várias outras situações. Para estudarmos probabilidade a fundo, é fundamental o domínio dos conceitos da análise combinatória, pois a probabilidade de um evento acontecer é a razão entre a contagem de todos os casos favoráveis sob a contagem de todos os casos possíveis.
Assim, problemas que envolvem probabilidade podem também necessariamente envolver uma situação de análise combinatória. Percebemos, então, que a análise combinatória é um pré-requisito para o aprendizado da probabilidade, oferecendo ferramentas importantes para a contagem tanto dos casos favoráveis como dos casos possíveis.
·         Exemplo
Em uma turma de Inglês, será sorteada para três estudantes uma viagem com tudo pago para a cidade de Caldas Novas. Sabendo que no curso há 12 alunos e que 5 são meninos, qual é a probabilidade de a dupla sorteada ser composta por duas meninas?
Resolução
Para calcular a probabilidade, precisamos antes contar todas os trios possíveis e também calcular todos os trios formadas por duas meninas. Como a ordem não é importante, podemos usar combinação.
1º passo – Todos os trios possíveis
·         n= 12 (todos os alunos)
·         p = 3 (quantidade de alunos a serem escolhidos)

2º passo – Todos os trios formados por duas meninas
·         n = 12 – 5→ n = 7 (total de meninas)
·         p=3 (quantidade de alunos a serem escolhidos)

3º passo - Cálculo da probabilidade

ATIVIDADES

TEMA 3 : Formação de Grupos com elementos de uma ou mais categorias – PG. 14

Atividade 17 da apostila , pagina

Whatsapp (14) 98122-3831 ou   Classroon

ATIVIDADES PARA A SEMANA DE 21/09 ATÉ 25/09

ATENÇÃO ALUNOS

ESTAMOS NA 8ª SEMANA DO 3º BIMESTRE

O CADERNO DO ALUNO VOL. 03 ESTÃO DISPONIVÉIS PARA SEREM RETIRADOS NA ESCOLA DESDE 01/09/2020

HORÁRIO DAS 10H ÁS 16H

TERÇA E QUINTA FEIRA ABERTO AO PÚBLICO

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, NÃO HÁ ESPAÇO PARA RESOLVER NO CADERNO

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.

“A persistência é o caminho do êxito.”

Charles Chaplin

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES DA 8ª SEMANA DO 3º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO PASSADA NA SEMANA ANTERIOR

CONTINUAÇÃO DAS ATIVIDADES

ATIVIDADES

TEMA 2 : Formação de filas sem e com elementos repetidos – PG. 10

Atividade 12 e 13 da apostila , pagina 12

Atividade 14, 15 e 16 apostila pagina 13

Atividade : simulado pag. 12 (foi entregue um simulado com gabarito com questões do ENEM.

Fazer a questão 30 (Enem 2017)

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 14/09 ATÉ 18/09

ATENÇÃO ALUNOS

ESTAMOS NA 7ª SEMANA DO 3º BIMESTRE

O CADERNO DO ALUNO VOL. 03 ESTÃO DISPONIVÉIS PARA SEREM RETIRADOS NA ESCOLA DESDE 01/09/2020

HORÁRIO DAS 10H ÁS 16H

Alunos que não fizeram a APP DO 2º BIMESTRE , vamos fazer, estou recebendo.

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, NÃO HÁ ESPAÇO PARA RESOLVER NO CADERNO

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES DA 7ª SEMANA DO 3º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO:

Análise Combinatória: A análise combinatória ou combinatória é a parte da Matemática que estuda métodos e técnicas que permitem resolver problemas relacionados com contagem. Muito utilizada nos estudos sobre probabilidade, ela faz análise das possibilidades e das combinações possíveis entre um conjunto de elementos.

O princípio fundamental da contagem, também chamado de princípio multiplicativo, postula que: “quando um evento é composto por n etapas sucessivas e independentes, de tal modo que as possibilidades da primeira etapa é x e as possibilidades da segunda etapa é y, resulta no número total de possibilidades de o evento ocorrer, dado pelo produto (x) . (y)”.

Em resumo, no princípio fundamental da contagem, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.

Exemplo

Uma lanchonete vende uma promoção de lanche a um preço único. No lanche, estão incluídos um sanduíche, uma bebida e uma sobremesa. São oferecidos três opções de sanduíches: hambúrguer especial, sanduíche vegetariano e cachorro-quente completo. Como opção de bebida pode-se escolher 2 tipos: suco de maçã ou guaraná. Para a sobremesa, existem quatro opções: cupcake de cereja, cupcake de chocolate, cupcake de morango e cupcake de baunilha. Considerando todas as opções oferecidas, de quantas maneiras um cliente pode escolher o seu lanche?

Solução: Podemos começar a resolução do problema apresentado, construindo uma árvore de possibilidades, conforme ilustrado abaixo:

Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis. Podemos ainda resolver o problema usando o princípio multiplicativo. Para saber quais as diferentes possibilidades de lanches, basta multiplicar o número de opções de sanduíches, bebidas e sobremesa.

Total de possibilidades: 3.2.4 = 24

Portanto, temos 24 tipos diferentes de lanches para escolher na promoção.

Tipos de Combinatória: O princípio fundamental da contagem pode ser usado em grande parte dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa.

Desta maneira, usamos algumas técnicas para resolver problemas com determinadas características. Basicamente há três tipos de agrupamentos: arranjos, combinações e permutações.

Antes de conhecermos melhor esses procedimentos de cálculo, precisamos definir uma ferramenta muito utilizada em problemas de contagem, que é o fatorial.

O fatorial de um número natural é definido como o produto deste número por todos os seus antecessores. Utilizamos o símbolo ! para indicar o fatorial de um número.

Define-se ainda que o fatorial de zero é igual a 1.

Exemplo:

O! = 1
1! = 1
3! = 3.2.1 = 6
7! = 7.6.5.4.3.2.1 = 5 040
10! = 10.9.8.7.6.5.4.3.2.1 = 3 628 800

Note que o valor do fatorial cresce rapidamente, conforme cresce o número. Então, frequentemente usamos simplificações para efetuar os cálculos de análise combinatória.

ATIVIDADES

TEMA 2:Formação de filas sem e com elementos repetidos – PG. 10

Atividade 07 e 08 da apostila , pagina 10

Atividade 09, 10 e 11 apostila pagina 11

Atividade : simulado pag. 12 (foi entregue um simulado com gabarito com questões do ENEM.

Fazer a questão 29 (Enem 2018)

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 08/09 ATÉ 11/09

ATENÇÃO ALUNOS

ESTAMOS NA 6ª SEMANA DO 3º BIMESTRE

O CADERNO DO ALUNO VOL. 03 ESTÃO DISPONIVÉIS PARA SEREM RETIRADOS NA ESCOLA DESDE 01/09/2020

HORÁRIO DAS 10H ÁS 16H

Alunos que não fizeram a APP DO 2º BIMESTRE , vamos fazer, estou recebendo.

AS ATIVIDADES SÃO DO CADERNO DO ALUNO VOL.3

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, NÃO HÁ ESPAÇO PARA RESOLVER NO CADERNO

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.

“A persistência nos estudos realiza o impossível.”

Profº. LEANDRO PICCINI

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES DA 6ª SEMANA DO 3º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 3

EXPLICAÇÃO:

Em resumo, no princípio fundamental da contagem, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.

Exemplo

Solução: Podemos começar a resolução do problema apresentado, construindo uma árvore de possibilidades, conforme ilustrado abaixo:

Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis.Podemos ainda resolver o problema usando o princípio multiplicativo. Para saber quais as diferentes possibilidades de lanches, basta multiplicar o número de opções de sanduíches, bebidas e sobremesa.

Total de possibilidades: 3.2.4 = 24

Portanto, temos 24 tipos diferentes de lanches para escolher na promoção.

Tipos de Combinatória: O princípio fundamental da contagem pode ser usado em grande parte dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa.

Desta maneira, usamos algumas técnicas para resolver problemas com determinadas características. Basicamente há três tipos de agrupamentos: arranjos, combinações e permutações.

Antes de conhecermos melhor esses procedimentos de cálculo, precisamos definir uma ferramenta muito utilizada em problemas de contagem, que é o fatorial.

O fatorial de um número natural é definido como o produto deste número por todos os seus antecessores. Utilizamos o símbolo ! para indicar o fatorial de um número.

Define-se ainda que o fatorial de zero é igual a 1.

Exemplo:

O! = 1
1! = 1
3! = 3.2.1 = 6
7! = 7.6.5.4.3.2.1 = 5 040
10! = 10.9.8.7.6.5.4.3.2.1 = 3 628 800

Note que o valor do fatorial cresce rapidamente, conforme cresce o número. Então, frequentemente usamos simplificações para efetuar os cálculos de análise combinatória.

ATIVIDADES DA APOSTILA VOL. 3

TEMA 1: Princípios aditivos e multiplicativos – PG. 07

Atividade 01 da apostila , pagina 07

Atividade 02, 03 e 04 apostila pagina 08

Atividade 05 e 06 da apostila, pagina 09

QUALQUER DÚVIDA, ENTRE EM CONTATO

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 30/08 ATÉ 04/09

ATENÇÃO ALUNOS

ESTAMOS NA 5ª SEMANA DO 3º BIMESTRE

O CADERNO DO ALUNO VOL. 03 ESTÃO DISPONIVÉIS PARA SEREM RETIRADOS NA ESCOLA Á PARTIR DE 01/09/2020 (terça-feira) ATÉ DIA 04/09/2020 (sexta-feira) NO HORÁRIO DAS 10H ÁS 16H

Alunos que não fizeram a APP DO 2º BIMESTRE , vamos fazer, estou recebendo.

AS ATIVIDADES SÃO DO CADERNO DO ALUNO VOL.2

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO, NÃO HÁ ESPAÇO PARA RESOLVER NO CADERNO

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESPONDER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.

“ O sucesso nasce do querer, da determinação e persistência em se chegar a um objetivo. Mesmo não atingindo o alvo, quem busca e vence obstáculos, no mínimo fará coisas admiráveis.”

JOSÉ DE ALENCAR

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES DA 5ª SEMANA DO 3º BIMESTRE

ATIVIDADES DA APOSTILA VOL. 2

A EXPLICAÇÃO DAS ATIVIDADES JÁ FORAM PASSADAS NA SEMANA DE 10 Á 14/08

ATIVIDADES DA APOSTILA VOL. 2

TEMA 3: RESOLUÇÕES DE SISTEMAS – PG.24

Atividade 32 da apostila , pagina 25

Atividade 33, 34 apostila pagina 26 ( não fazer 35 e 36)

Atividade 41 da apostila, pagina 29

BOM TRABALHO A TODOS

QUALQUER DÚVIDA, ENTRE EM CONTATO

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 17/08 ATÉ 21/08

ATENÇÃO ALUNOS

ESTAMOS NA 3ª SEMANA DO 3º BIMESTRE

AS ATIVIDADES SÃO DO CADERNO DO ALUNO VOL.2

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES SÃO PARA SER FEITAS NO CADERNO (SE NÃO HOUVER ESPAÇO NA APOSTILA)

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 17 á 24/08/2020

- COPIAR SOMENTE O EXERCÍCIO E RESOLVER

- ENVIAR AS ATIVIDADES PELO WhatsApp OU Classroon , ENVIAR A FOTO.

VAMOS JUNTOS VENCER A DISTÂNCIA, SOMOS MAIS FORTES

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES DA 2ª SEMANA DO 3º BIMESTRE

DE 17 Á 21/08/2020

ATIVIDADES DA APOSTILA VOL. 2

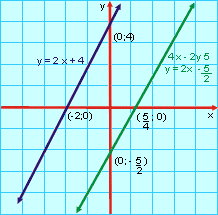
EXPLICAÇÃO: SISTEMAS DE EQUAÇÕES LINEARES

1. Métodos de resolução

No plano, duas retas não paralelas encontram-se exatamente em um ponto. A partir das equações das retas podemos determinar as coordenadas desse ponto. Por exemplo, sejam as retas de equações:

x + 2y = 4

2x + y = 5

Note que as coordenadas do ponto de intersecção P devem satisfazer cada uma das equações. Para determiná-las devemos resolver o sistema formado pelas equações das duas retas.

Descrevemos dois métodos para a resolução do sistema.

= - 2 . 1 + 4

= 2

A solução do sistema é x = 2 e y = 1, ou o par (2; 1). Na figura acima, o ponto P tem coordenadas (2; 1).

2° método - O método da adição

1° passo: As equações devem ser escritas na forma geral. No caso, as equações já estão escritas nessa forma - esse 1° passo é desnecessário.

Daí,

4x - 4x - 8 = 5

-8 = 5 !

Mas, -8

5 ; isso mostra que as equações do sistema são independentes e que o sistema é impossível.

Os gráficos das equações são retas paralelas.

Somando membro a membro as equações, vem

0x + 0y = 0

0 = 0 !

Note que ambas incógnitas x e y foram eliminadas. A veracidade do resultado 0 = 0 mostra que as equações do sistema são dependentes e que o sistema é possível.

As equações do sistema são equivalentes: a primeira equação multiplicada por -3 resulta na segunda. Os gráficos das duas equações coincidem. Qualquer par ordenado que satisfaz uma equação também satisfaz a outra. O sistema tem infinitas soluções.

ATIVIDADES

Atividade 25, 26 e 27 da apostila , pagina 22

Atividade 28,29 30 e 31 apostila pagina 23

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 10/08 ATÉ 17/08

ATENÇÃO ALUNOS

ESTAMOS NA 2ª SEMANA DO 3º BIMESTRE

OS ALUNOS QUE NÃO ENTREGARAM ATIVIDADES, OU TEM ATIVIDADES EM ATRASO PARA SER ENTREGUE, POR FAVOR ENVIAR COM URGENCIA.

A AAP DE MATEMÁTICA ESTÁ A DISPOSIÇÃO DOS ALUNOS PARA SEREM RETIRADAS NA ESCOLA DAS 10H AS 16H . CASO O ALUNO QUEIRA FAZER DE FORMA ONLINE O LINK ESTÁ DISPONÍVEL NO BLOG DA ESCOLA E NO CLASSROON

ORIENTAÇÕES A SEREM SEGUIDAS

- AS ATIVIDADES QUE TIVER ESPAÇO NA APOSTILA, RESOLVER NELA MESMA, SE NÃO HOUVER ESPAÇO FAZER NO CADERNO (DA SEGUINTE FORMA)

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 20 á 24/07/2020

- AS ATIVIDADES PODEM SER ENTREGUES PELO WhatsApp PARTICULAR OU PELO CLASSROON

- TANTO PELO WhatsApp OU CLASSROON , ENVIAR A FOTO.

- A NOTA É COMPOSTA PELA ENTREGA DAS ATIVIDADES, PONTUALIDADE E COMPROMETIMENTO

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 03/08 ATÉ 07/08

ATENÇÃO

CAROS ALUNOS, ESTÁ SEMANA NOSSA ATIVIDADES SERÁ A REALIZAÇÃO DA PROVA AAP JÁ DISPONIVÉL PARA SER RETIRADA NA ESCOLA.

ORIENTAÇÕES:

- A PROVA É PARA SER RETIRADA NA ESCOLA NO HORÁRIO DAS 10H ás 16H DE SEGUNTA A sexta-feira

- PREENCHER O GABARITO E OS DADOS CORRETAMENTE DE FORMA LEGÍVEL.

- ENVIAR O GABARITO PELO WHATSAAP PESSOAL OU PELO CLASSROON

- A DATA DE ENTREGA É DIA 10/08/2020

- QUALQUER PROBLEMA ENTRAR EM CONTATO NO WHATSAAP PARTICULAR

AVISO: FAREI UM GRUPO SÓ DE MATEMÁTICA A PARTIR DESTA PRIMEIRA SEMANA DO 3º BIMESTRE

REFORÇANDO AS ATIVIDADES DESTA SEMANA

RETIRAR A PROVA AAP NA ESCOLA E FAZER ENTREGANDO ATÉ DIA 10/08/2020

OBS: MEUS CONTATOS DESDE O 1º BIMESTRE SÃO:

Whatsapp (14) 98122-3831

e-mail: neia637@hotmail.com E CLASSROOM

ATIVIDADES PARA A SEMANA DO DIA 27/07 ATÉ 31/07

ATENÇÃO ALUNOS

O BIMESTRE SE ENCERRA NA QUARTA-FEIRA, DIA 29/07/2020

OS ALUNOS QUE NÃO ENTREGARAM ATIVIDADES, OU TEM ATIVIDADES EM ATRASO PARA SER ENTREGUE, O PRAZO FINAL É ATÉ QUARTA-FEIRA, DIA 29/07/2020

AOS ALUNOS QUE ESTÃO EM DIA COM AS ATIVIDADES, TEMOS AULAS NO CENTRO DE MIDIA E FAREMOS AS ATIVIDADES PROPOSTAS NAS AULAS. ESTOU TAMBÉM A DISPOSIÇÃO PARA QUE SE HOUVER DÚVIDAS EM ALGUMA ATIVIDADE, ME CHAMAR NO WHATSAAP PARTICULAR (98122-3831)

OBS: VÁRIOS ALUNOS NÃO TEM SEGUIDO ESTÁS ORIENTAÇÕES

SEGUIR AS ORIENTAÇÕES

- AS ATIVIDADES QUE TIVER ESPAÇO NA APOSTILA, RESOLVER NELA MESMA, SE NÃO HOUVER ESPAÇO FAZER NO CADERNO (DA SEGUINTE FORMA)

- NA PRIMEIRA LINHA DA FOLHA CONSTAR: NOME, SÉRIE E COLOCAR “ ATIVIDADES DA SEMANA Ex: de 20 á 24/07/2020

- AS ATIVIDADES PODEM SER ENTREGUES PELO WhatsApp PARTICULAR OU PELO CLASSROON

- TANTO PELO WhatsApp OU CLASSROON , ENVIAR A FOTO.

Whatsapp (14) 98122-3831 ou Classroon

ATIVIDADES PARA A SEMANA DO DIA 20/07 ATÉ 24/07

PRAZO DE ENTREGA

ATÉ 27/07/2020 através do whatsapp particular ou CLASSROON

Atividades da semana 20 á 24/07/2020

EXPLICAÇÃO E EXEMPLOS: foi passado na semana anterior

- AS ATIVIDADES CONTINUAM DE MATRIZES NA APOSTILA

- NA APOSTILA NÃO TEM ESPAÇO PARA OS CALCULOS, FAÇAM NO CADERNO

- AO ENVIAR AS ATIVIDADES, NÃO ESQUEÇAM DE COLOCAR O NOME, SÉRIE E A SEMANA DAS ATIVIDADES QUE ESTÃO SENDO ENVIADAS

- AS ATIVIDADES PODEM SER FOTOGRAFADAS E ENVIADAS PELO WHATSAAP PARTICULAR OU PELO CLASSROON.

BOA SEMANA A TODOS

ATIVIDADES – continuação matrizes

Na apostila, pagina 13, 14 e 15 Atividade 16, 17, 18 e 19

Obs: Na apostila não tem espaço para resolver o exercício, faça no caderno.

Qualquer duvida me chame no particular.

Whatsapp (14) 98122-3831 ou

Pelo Classroon

ATIVIDADES PARA A SEMANA DO DIA 13/07 ATÉ 17/07

EXPLICAÇÃO E EXEMPLOS

Multiplicação de Matrizes

A multiplicação de matrizes é realizada de acordo com a seguinte condição: o número de colunas da 1ª matriz deve ser igual ao número de linhas da 2ª matriz. Observe alguns modelos de matrizes que podem ser multiplicadas, considerando o formato m x n.

A_4x3 * B_3x1

A_4x2 * B_2x3

A_1x2 * B_2x2

A_3x4 * B_4x3

Nesse modelo de multiplicação, os métodos são mais complexos. Dessa forma, precisamos ter muita atenção na resolução de uma multiplicação de matrizes. Vamos através de exemplos, demonstrar como efetuar tais cálculos. A operação deverá ser feita multiplicando os membros da linha da 1º matriz pelos membros da coluna da 2º matriz, onde os elementos devem ser somados, constituindo um único item posicional da matriz. Observe um modelo padrão de multiplicação:

Exemplo 1

ATIVIDADES - continuação

Na apostila, pagina 12, 13, Atividade 13, 14, 15

Obs: Na apostila não tem espaço para resolver o exercício, faça no caderno.

Qualquer duvida me chame no particular.

Whatsapp (14) 98122-3831

Pelo classroon

ATIVIDADES PARA A SEMANA DO DIA 06/07 ATÉ 10/07

EXEMPLOS

Determine a matriz A = [a_ij ]_2x2, que possui a seguinte lei de formação a_ij = j² – 2i. Dos dados do enunciado, temos que a matriz A é de ordem dois por dois, ou seja, possui duas linhas e duas colunas, logo:

Além disso, foi dada a lei de formação da matriz, ou seja, a cada elemento satisfaz-se a relação a_ij = j² – 2i. Substituindo os valores de i e j na fórmula, temos:

a₁₁ = (1)² - 2(1) = -1

a₁₂ = (2)² - 2(1) = 2

a₂₁ = (1)² - 2(2) = -3

a₂₂= (2)² - 2(2) = 0

Portanto, a matriz A é:

ATIVIDADES - continuação

Na apostila, pagina 10, 11 e 12 Atividade 9, 10, 11 e 12

Obs: Na apostila não tem espaço para resolver o exercício, faça no caderno.

Qualquer duvida me chame no particular.

Whatsapp (14) 98122-3831

Pelo classroon

ATIVIDADES PARA A SEMANA DO DIA 29/06 ATÉ 03/07

EXEMPLOS

Além disso, foi dada a lei de formação da matriz, ou seja, a cada elemento satisfaz-se a relação a_ij = j² – 2i. Substituindo os valores de i e j na fórmula, temos:

a₁₁ = (1)² - 2(1) = -1

a₁₂ = (2)² - 2(1) = 2

a₂₁ = (1)² - 2(2) = -3

a₂₂= (2)² - 2(2) = 0

Portanto, a matriz A é:

ATIVIDADES

Na apostila, pagina 8 e 9, Atividade 4, 5, 6, 7 e 8

Obs: Na apostila não tem espaço para resolver o exercício, faça no caderno.

Qualquer duvida me chame no particular.

PRAZO DE ENTREGA

ATÉ 06/07/2020 através do whatsapp particular ou Classroon

Whatsapp (14) 98122-3831

Pelo classroon

Anexe aqui as atividades que os alunos desenvolverão e serão postadas no BLOG da escola

· Lembrando

DELIBERAÇÃO CEE 155/17

TÍTULO III DO PROCESSO DE AVALIAÇÃO ESCOLAR

Art. 16 - As propostas pedagógicas das escolas devem indicar com clareza as aprendizagens que devem ser asseguradas aos alunos nos níveis fundamental e médio da Educação Básica, nas diferentes áreas e componentes curriculares.

Parágrafo único –

A avaliação do rendimento escolar terá como referência básica o conjunto dessas aprendizagens.

Art. 17 - A avaliação dos alunos, a ser realizada pelos professores e pela escola como parte integrante da proposta curricular e da implementação do currículo, é redimensionadora da ação pedagógica e deve:

I - assumir um caráter processual, formativo e participativo, ser contínua, cumulativa e diagnóstica, com vistas a:

a) identificar potencialidades e dificuldades de aprendizagem e detectar problemas de ensino;

b) subsidiar decisões sobre a utilização de estratégias e abordagens de acordo com as necessidades dos alunos, criar condições de intervir de modo imediato e a mais longo prazo para sanar dificuldades e redirecionar o trabalho docente;

II - utilizar vários instrumentos e procedimentos, tais como a observação, o registro descritivo e reflexivo, os trabalhos individuais e coletivos, os portfólios, exercícios, provas, questionários, dentre outros, tendo em conta a sua adequação à faixa etária e às características de desenvolvimento do educando;

III - fazer prevalecer os aspectos qualitativos da aprendizagem do aluno sobre os quantitativos, bem como os resultados ao longo do período sobre os de provas finais, quando essas ocorrerem, tal como determina a alínea “a” do inciso V do art. 24 da Lei nº 9.394/96.

ATIVIDADES PARA A SEMANA DO DIA 26/05 ATÉ 29/05

EXPLICAÇÃO E EXEMPLOS

Passado na semana passada

ATIVIDADES

Na apostila, pagina 7 e 8, Atividade 2 e 3

Obs: Na apostila não tem espaço para resolver o exercício, faça no caderno.

Qualquer duvida me chame no particular.

Whatsapp (14) 98122-3831 ou

e-mail: neia637@hotmail.com

RESPONDER O LINK ABAIXO

https://classroom.google.com/c/MTM2NzA5MDE1NzAz/a/MTE0Njk5NzgzMzE2/details

ATIVIDADES PARA A SEMANA DO DIA 15/06 ATÉ 19/06

EXPLICAÇÃO E EXEMPLOS

Matrizes são organizações de informações numéricas em uma tabela retangular formada por linhas e colunas. Essa organização em uma tabela facilita que se possa efetuar vários cálculos simultâneos com as informações contidas na matriz.

Definição de matrizes: Toda matriz tem o formato m x n (leia-se: m por n, com m e n ∈ N*), onde m é o número de linhas e n o número de colunas.

Representação de matrizes: Existem diversas maneiras de representarmos matrizes, veja quais são:

Colchetes: [ ]
Parênteses: ( )
Barras Simples: | |
Barras Duplas: || ||

Essas são as representações mais comuns que encontramos na literatura.

Exemplos:

Elementos de uma matriz: Seja a matriz genérica A_mxn, isto é, m representa as linhas e n o número de colunas. Então, temos:

Dessa forma, os elementos da matriz A são indicados por a_ij, onde o i representa o índice da linha e j representa o índice da coluna para o elemento em questão. Assim, para localizarmos um elemento na coluna, procuramos o número da linha e da coluna, esses números são os índices i e j. Pela imagem acima, veja que as linhas são numeradas de cima para baixo, enquanto que as colunas são numeradas da esquerda para a direita.

Exemplos:

a₁₁ representa o elemento da linha 1 e coluna 1.
a₃₂ representa o elemento da linha 3 e coluna 2.
a₂₂ representa o elemento da linha 2 e coluna 2.
a_mn representa o elemento da linha m e coluna n.

Seja a matriz

assim:

a₁₁ representa o elemento 1.
a₁₂ representa o elemento 4.
a₁₃ representa o elemento 0.
a₂₁ representa o elemento -2.
a₂₂ representa o elemento 4.
a₂₃ representa o elemento 3.

Uma matriz também pode ser representada por uma forma abreviada de forma que possamos escrevê-la facilmente.

Exemplo: Considere a matriz M = [a_ij]_2×3, tal que a_ij = i + j. Escreva a matriz M.

Primeiramente vamos verificar as informações passadas. Observe que teremos uma matriz retangular, com 2 linhas e 3 colunas. Os elementos da matriz é a soma dos índices (posição) das linhas e colunas. Assim Escrevendo os elementos:

a₁₁ = 1 + 1 = 2.
a₁₂ = 1 + 2 = 3.
a₁₃ = 1 + 3 = 4.
a₂₁ = 2 + 1 = 3.
a₂₂ = 2 + 2 = 4.
a₂₃ = 2 + 3 = 5.

Então a matriz M é:

ATIVIDADES

Na apostila, pagina 7, Atividade 1

Obs: Na apostila não tem espaço para resolver o exercício, faça no caderno.

Whatsapp (14) 98122-3831 ou

e-mail: neia637@hotmail.com

ATIVIDADES PARA A SEMANA DO DIA 08/06 ATÉ 12/06

ATIVIDADES

1 - No lançamento de dois dados perfeitos, qual a probabilidade de que a soma dos resultados obtidos seja igual a 6?

2 - Considerando todos os divisores positivos do numeral 60, determine a probabilidade de escolhermos ao acaso, um número primo.

3 - Em uma existem bolas enumeradas de 1 a 15. Qualquer uma delas possui a mesma chance de ser retirada. Determine a probabilidade de se retirar uma bola com número nas seguintes condições:
a) par
b) primo
c) par ou primo
d) par e primo

4 - Uma moeda é lançada 10 vezes. Determine a probabilidade de sair “coroa” 7 vezes.

Whatsapp (14) 98122-3831 ou

e-mail: neia637@hotmail.com

ATIVIDADES PARA A SEMANA DO DIA 26/05 ATÉ 29/05

ATENÇÃO ALUNOS

ESTÁ SEMANA ESTAREMOS DANDO UMA OLHA NOS CONTEÚDOS ESTUDADOS PARA TIRAR AS DÚVIDAS E TERMINANDO AS ATIVIDADES PARA SEREM ENVIADAS ATÉ AMANHÃ DIA 27/05/2020 PARA FECHAMENTO DO 1º BIMENSTRE.

Obs: APROVEITEM PARA SE ORGANIZAR SEUS HORÁRIOS E AS ATIVIDADES PARA O 2º BIMESTRE. NÃO DEIXE ACOMULAR RESPEITANDO OS PRAZOS DE ENTREGA.

Whatsapp (14) 98122-3831 ou

e-mail: neia637@hotmail.com

ATIVIDADES PARA A SEMANA DO DIA 18/05 ATÉ 22/05

ATENÇÃO ALUNOS

ESTÁ SEMANA FAREMOS A AVALIAÇÃO QUE ESTÁ DISPONIVEL JUNTO COM O KIT PARA TODOS NA ESCOLA. QUEM NÃO RETIROU É SÓ COMPARECER E RETIRAR NA ESCOLA.

Obs: Se vocês tiverem conhecimento de algum colega que não está no grupo de whatsapp da escola, ou não está conseguindo entrar no Blog da escola, ou mesmo com dificuldades de acesso de internet, peça para entrar em contado que estaremos vendo com a direção como podemos ajudar. Pode passar o meu telefone ou ligar na escola.

ATIVIDADES

RESOLVER A AVALIAÇÃO AAP E ENVIAR O GABARITO PELO :

Whatsapp (14) 98122-3831 ou

e-mail: neia637@hotmail.com

ATIVIDADES PARA A SEMANA DO DIA 11/05 ATÉ 15/05

MÉDIA, MODA E MEDIANA : são medidas obtidas de conjuntos de dados que podem ser usadas para representar todo o conjunto. A tendência dessas medidas é resultar em um valor central. Por essa razão, elas são chamadas de medidas de centralidade.

Moda - É chamado de moda o dado mais frequente de um conjunto. Exemplo: Em uma escola de música, as turmas são formadas por apenas 8 alunos. Na turma “A”, estão matriculados Mateus, Mateus, Rodrigo, Carolina, Ana, Ana, Ana e Teresa.

Observe que há dois meninos chamados de Mateus e três meninas chamadas de Ana. O nome que mais se repete é Ana e, por isso, é a moda desse conjunto de dados.

Agora um exemplo com números: em uma escola de música, os oito alunos da turma “A” possuem as seguintes idades: 12 anos, 13 anos, 13 anos, 12 anos, 11 anos, 10 anos, 14 anos e 11 anos.

Perceba que as idades 11, 12 e 13 repetem-se o mesmo número de vezes e nenhuma idade aparece mais que essas três. Nesse caso, o conjunto possui três modas (11, 12 e 13) e é chamado de trimodal.

Também podem existir conjuntos bimodais, isto é, com duas modas; amodais, com nenhuma moda etc.

Mapa Mental: Medidas de Tendência Central

Mediana : Se o conjunto de informações for numérico e estiver organizado em ordem crescente ou decrescente, a sua mediana será o número que ocupa a posição central da lista. Considere que a escola de música já citada possui nove professores e que suas idades são: 32 anos, 33 anos, 24 anos, 31 anos, 44 anos, 65 anos, 32 anos, 21 anos e 32 anos

Para encontrar a mediana das idades dos professores, devemos organizar a lista de idades em ordem crescente:

21, 24, 31, 32, 32, 32, 33, 44 e 65

Observe que o número 32 é o quinto. À sua direita, existem outras 4 idades, assim como à esquerda. Logo, 32 é a mediana da lista das idades dos professores.

21, 24, 31, 32, 32, 32, 33, 44, 65

Se a lista possuir um número par de informações, para encontrar a mediana (M_a), devemos encontrar os dois valores centrais (a₁ e a₂) da lista, somá-los e dividir o resultado por 2.

M_a = a₁ + a₂
2

Se as idades dos professores fossem 19 anos, 19 anos, 18 anos, 22 anos, 44 anos, 45 anos, 46 anos, 46 anos, 47 anos e 48 anos, a lista crescente com as duas medidas centrais seria:

8, 19, 19, 22, 44, 45, 46, 46, 47, 48

Observe que a quantidade de informações à direta e à esquerda desses dois números é exatamente a mesma. A mediana desse conjunto de dados é, portanto:

M_a = a₁ + a₂
2

M_a = 44 + 45
2

M_a = 89
2

M_a = 44,5 anos

Média

Média (M), mais precisamente chamada de média aritmética simples, é o resultado da soma de todas as informações de um conjunto de dados dividida pelo número de informações que foram somadas. A média aritmética simples entre 14, 15 e 25, por exemplo, é a seguinte:

M = 14 + 15 + 25
3

Como há três dados na lista, dividimos a soma desses dados pelo número 3. O resultado é:

M = 54
3

M = 18

A média é a medida de centralidade mais usada por ser a que mescla de maneira mais uniforme os valores mais baixos e os mais altos de uma lista. No conjunto anterior, por exemplo, a mediana é igual a 44,5, mesmo com tantas idades próximas de 20 anos. Observe a média aritmética simples desse mesmo conjunto:

M = 18 + 19 + 19 + 22 + 44 + 45 + 46 + 46 + 47 + 48
10

M = 35,4 anos

Média ponderada

A média ponderada (M_p) é uma extensão da média simples e considera pesos para as informações do conjunto de dados. É feita por meio da soma do produto de uma informação pelo seu respectivo peso e, em seguida, a divisão desse resultado pela soma de todos os pesos usados.

Considere como exemplo os dados na tabela a seguir, que contém uma lista com as idades dos alunos do sexto ano da escola A. Vamos calcular a média das idades.

Existe a possibilidade de calcular a média simples ao somar 10 anos quatro vezes, 11 anos quinze vezes etc. Entretanto, por meio de uma média ponderada, podemos considerar a quantidade de alunos com 11 anos como o peso dessa idade nessa sala de aula; a quantidade de alunos que possuem 10 anos como peso dessa idade, e assim por diante até que todas as idades tenham sido somadas. Assim, o cálculo da média ponderada seria:

M_p = 4·10 + 15·11 + 10·12 + 1·13
4 + 15 + 10 + 1

M_p = 40 + 165 + 120 + 13
30

M_p = 338
30

M_p = 11,26 anos.

ATIVIDADES

Atividade 1 – FAÇA UMA PESQUISA SOBRE A TORRE DE HANOI COM DOIS EXERCICIOS RESOLVIDOS COMO EXEMPLO.

Atividade 2 - Determine a média, moda e mediana do seguinte conjunto de dados:

A = {2, 5, 1, 8, 12, 9, 10, 2}

Atividade 3 - Calcule a média simples do conjunto de dados:

a) {1,22; 4,302; 9,012; 100,91}

b) {5; 8; 4; 6}

c) {1,3; 9,1; 2,7; 8,0; 30,2}

Atividade 4 - Os dados da tabela abaixo são referentes as idades dos alunos de uma determinada disciplina.

Calcule a media das idades, a mediana das idades e a idade modal dos alunos da disciplina.

ATIVIDADES PARA A SEMANA DO DIA 04/05 ATÉ 08/05

A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos.

Ela é utilizada também em outras áreas de estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.

Funções Trigonométricas

As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.

As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:

Lê-se cateto oposto sobre a hipotenusa.

Lê-se cateto adjacente sobre a hipotenusa.

Lê-se cateto oposto sobre cateto adjacente.
EXEMPLO: A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?
Considere:
sen 40º = 0,64
cos 40º = 0,77
tg 40º = 0,84

Vamos começar o exercício representando na figura a altura do avião. Para isso, basta desenhar uma reta perpendicular à superfície e que passa pelo ponto onde o avião se encontra.

Notamos que o triângulo indicado é retângulo e a distância percorrida representa a medida da hipotenusa deste triângulo e a altura do cateto oposto ao ângulo dado.
Portanto, usaremos o seno do ângulo para encontrar a medida da altura:
Assim, ao percorrer 8 000 m, o avião se encontra a 5 120 m de altura.

ATIVIDADES

Atividade 1 – Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2 000 metros em linha reta, qual será a altura atingida pelo avião, aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º = 0,364)

Atividade 2 - Um avião decola, percorrendo uma trajetória retilínea, formando com o solo, um ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1 000 metros, qual a altura atingida pelo avião?

Atividade 3 - Determine a medida x e y do triângulo retângulo a seguir. (Considere: sen(62,1°) = 0,88; cos(62,1°) = 0,47)

ATIVIDADES PARA A SEMANA DE 27/04 ATÉ 01/05

Para resolver exercícios sobre progressões, devemos aplicar as fórmulas do termo geral e da soma dos termos de uma PA e de uma PG.

EX: Encontre o termo geral da progressão aritmética (PA) abaixo:

A = (3, 7, ...) Apesar de a sequência apresentar apenas dois elementos, já podemos destacar dois termos importantes. Temos o primeiro elemento (a₁ = 3) e ainda a razão, que é dada pela diferença de um termo pelo termo imediatamente anterior. Portanto, a razão r é dada por r = 7 – 3 = 4. Dessa forma, é possível determinar a fórmula de seu termo geral:

a_n = a₁ + (n – 1).r
a_n = 3 + (n – 1).4
a_n = 3 + 4n – 4
a_n = 4n – 1

Então, o termo geral da PA (3, 7, …) é a_n = 4n – 1.

Atividade 1 – A soma dos 20 termos de uma PA é 500. Se o primeiro termo dessa PA é 5, qual é a razão r dessa PA?

Atividade 2 - (UF – CE) A soma dos 15 primeiros termos de uma progressão aritmética é 150. O 8° termo dessa PA é:

a) 10

b) 15

c) 20

d) 25

e) 30

Atividade 3 - Um jardim tem uma torneira e dez roseiras dispostas em linha reta. A torneira dista 50 m da primeira roseira e cada roseira dista 2 m da seguinte. Um jardineiro, para regar as roseiras, enche um balde na torneira e despeja seu conteúdo na primeira. Volta à torneira e repete a operação para cada roseira seguinte. Após regar a última roseira e voltar à torneira para deixar o balde, ele terá andado:

a) 1200 m.

b) 1180 m.

c) 1130 m.

d) 1110 m.

e) 1000 m.

Atividade 4 – Várias tábuas iguais estão em uma madeireira. A espessura de cada tábua é 0,5 cm. Forma-se uma pilha de tábuas colocando-se uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha.

Determine ao final de nove dessas operações:

a) quantas tábuas terá a pilha;

b) a altura, em metros, da pilha.

Atividade 5 – Determine a soma dos 10 primeiros termos da PG (1, 3, 9, 27)

REVISÃO

Resolva as equações de 2 grau através da formula de bhaskara:

a) 2x² + x – 3 = 0

b) – 3x² + 18x – 15 = 0

c) – 2x² + 3x + 5 = 0

d) 3x² – x – 1 = 0

e) 3x² – 2x – 2 = 0

f) x²-x-20=0

g) x²-3x-4=0

h) 4x² + 8x + 6 = 0

i) x² – 4x – 5 = 0

j) x² + ax + b = 0

Exercícios Sobre Função Do 2° Grau

Para resolver exercícios sobre função do 2º grau, pode-se utilizar a fórmula de Bhaskara ou isolar a variável x.

1-) Calcule o valor de f(x) = x² + 3x – 10 para que f(x) = 0

2-) Calcule o valor de 5x² + 15x = 0 para que f(x) = 0

terça-feira, 8 de dezembro de 2020

MATEMÁTICA

EXPLICAÇÃO: TEOREMA DE PITÁGORAS

Fórmula do teorema de Pitágoras

EXPLICAÇÃO: TEOREMA DE PITÁGORAS

Fórmula do teorema de Pitágoras

EXPLICAÇÃO:

EXPLICAÇÃO: PRISMAS: UMA FORMA DE OCUPAR O ESPAÇO

EXPLICAÇÃO: ESTUDANDO AS PROBABILIDADES

EXPLICAÇÃO: Análise Combinatória, Probabilidade

Princípio fundamental da contagem

Fatorial de um número

Tipos de agrupamentos

· Permutação

· Arranjo

Analisando o problema:

· Combinação

Analisando o problema:

Análise combinatória e probabilidade

EXPLICAÇÃO: Análise Combinatória, Probabilidade

Princípio fundamental da contagem

Fatorial de um número

Tipos de agrupamentos

· Permutação

· Arranjo

Analisando o problema:

· Combinação

Analisando o problema:

Análise combinatória e probabilidade

EXPLICAÇÃO: Análise Combinatória, Probabilidade

Princípio fundamental da contagem

Fatorial de um número

Tipos de agrupamentos

· Permutação

· Arranjo

Analisando o problema:

· Combinação

Analisando o problema:

Análise combinatória e probabilidade

Tipos de Combinatória: O princípio fundamental da contagem pode ser usado em grande parte dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa.

Tipos de Combinatória: O princípio fundamental da contagem pode ser usado em grande parte dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa.

Multiplicação de Matrizes

A multiplicação de matrizes é realizada de acordo com a seguinte condição: o número de colunas da 1ª matriz deve ser igual ao número de linhas da 2ª matriz. Observe alguns modelos de matrizes que podem ser multiplicadas, considerando o formato m x n.

Definição de matrizes: Toda matriz tem o formato m x n (leia-se: m por n, com m e n ∈ N*), onde m é o número de linhas e n o número de colunas.

Representação de matrizes: Existem diversas maneiras de representarmos matrizes, veja quais são:

Elementos de uma matriz: Seja a matriz genérica Amxn, isto é, m representa as linhas e n o número de colunas. Então, temos:

Moda - É chamado de moda o dado mais frequente de um conjunto. Exemplo: Em uma escola de música, as turmas são formadas por apenas 8 alunos. Na turma “A”, estão matriculados Mateus, Mateus, Rodrigo, Carolina, Ana, Ana, Ana e Teresa.

Mapa Mental: Medidas de Tendência Central

Média

Média ponderada

Nenhum comentário:

Postar um comentário

Elementos de uma matriz: Seja a matriz genérica A_mxn, isto é, m representa as linhas e n o número de colunas. Então, temos: